Welcome post
Across the world, the combined ratio is too high is not by chance that non-life companies face a profitability problem.
An insurance company has a production based on a 'raw material’, whose cost is not known at the time of the insurance. So, they use a lot of actuarial models to find this cost.
Then, insurance companies sum all the other expenses and put a margin on top. And they say they have a "price".
But… summing up all costs loadings only gives ‘the total cost’, not a price!
How should an insurance company define it’s price?
Our blog tells the story.
Find us at: http://dataxl.mozello.com/
Our archive is here.
Some R models about coronavirus
## Dados da wikipedia.
# https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_Italy
# https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_Germany
# https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_France
# https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_Spain
library(Rcmdr)
library( "systemfit" )
library( MASS )
###################################
#BOX COX - teste ##
#-adequado para ver quando há abandono de exponencial (lambda >0 )
###################################
#https://stackoverflow.com/questions/33999512/how-to-use-the-box-cox-power-transformation-in-r
powerTransform <- function(y, lambda1, lambda2 = NULL, method = "boxcox") {
boxcoxTrans <- function(x, lam1, lam2 = NULL) {
# if we set lambda2 to zero, it becomes the one parameter transformation
lam2 <- ifelse(is.null(lam2), 0, lam2)
if (lam1 == 0L) {
log(y + lam2)
} else {
(((y + lam2)^lam1) - 1) / lam1
}
}
switch(method
, boxcox = boxcoxTrans(y, lambda1, lambda2)
, tukey = y^lambda1
)
}
InversePowerTransform <- function(y, lam) {
return( (y*lam+1)^(1/lam))
}
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
IT<-boxcox((IT)~Dias, data=Dataset)
lambda.IT <- IT$x[which.max(IT$y)]
IT <- lm(powerTransform(IT, lambda.IT) ~ Dias,data=Dataset)
summary(IT)
GR<-boxcox((GR)~Dias, data=Dataset)
(lambda.GR <- GR$x[which.max(GR$y)])
GR <- lm(powerTransform(GR, lambda.GR) ~ Dias,data=Dataset)
summary(GR)
FR<-boxcox((FR)~Dias, data=Dataset)
(lambda.FR <- FR$x[which.max(FR$y)])
FR <- lm(powerTransform(FR, lambda.FR) ~ Dias,data=Dataset)
summary(FR)
SP<-boxcox((SP)~Dias, data=Dataset)
(lambda.SP <- SP$x[which.max(SP$y)])
SP <- lm(powerTransform(SP, lambda.SP) ~ Dias,data=Dataset)
summary(SP)
#PT<-boxcox((PT)~Dias, data=Dataset[20-7:20,])
PT<-boxcox((PT)~Dias, data=Dataset)
(lambda.PT <- PT$x[which.max(PT$y)])
PT <- lm(powerTransform(PT, lambda.PT) ~ Dias,data=Dataset)
summary(PT)
par(oldpar)
###################################
#MODELO BOX COX previsão (depende do modulo anterior para obtenção de Lambda)
###################################
IT <- lm(powerTransform(IT, lambda.IT) ~ Dias,data=Dataset)
GR <- lm(powerTransform(GR, lambda.GR) ~ Dias,data=Dataset)
FR <- lm(powerTransform(FR, lambda.FR) ~ Dias,data=Dataset)
SP <- lm(powerTransform(SP, lambda.SP) ~ Dias,data=Dataset)
PT <- lm(powerTransform(PT, lambda.PT) ~ Dias,data=Dataset)
summary(IT)
summary(GR)
summary(FR)
summary(SP)
summary(PT)
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 2))
plot(PT)
par(oldpar)
dev.off()
#previsão
Dataset$IT.pred.bc<-InversePowerTransform(predict(IT,newdata=Dataset),lambda.IT)
Dataset$GR.pred.bc<-InversePowerTransform(predict(GR,newdata=Dataset),lambda.GR)
Dataset$FR.pred.bc<-InversePowerTransform(predict(FR,newdata=Dataset),lambda.FR)
Dataset$SP.pred.bc<-InversePowerTransform(predict(SP,newdata=Dataset),lambda.SP)
Dataset$PT.pred.bc<-InversePowerTransform(predict(PT,newdata=Dataset),lambda.PT)
#32 30 27 30 24
Dataset$IT.dia33.CasosPorMilhão<-c(Dataset[1:32,]$IT,Dataset[33:106,]$IT.pred.bc)
Dataset$GR.dia30.CasosPorMilhão<-c(Dataset[1:30,]$GR,Dataset[31:106,]$GR.pred.bc)
Dataset$FR.dia27.CasosPorMilhão<-c(Dataset[1:27,]$FR,Dataset[28:106,]$FR.pred.bc)
Dataset$SP.dia30.CasosPorMilhão<-c(Dataset[1:30,]$SP,Dataset[31:106,]$SP.pred.bc)
Dataset$PT.dia24.CasosPorMilhão<-c(Dataset[1:24,]$PT,Dataset[25:106,]$PT.pred.bc)
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(1, 3))
with(Dataset[1:24,], lineplot(Dias,
PT.dia24.CasosPorMilhão,
IT.dia33.CasosPorMilhão ,
SP.dia30.CasosPorMilhão,
GR.dia30.CasosPorMilhão,
FR.dia27.CasosPorMilhão))
with(Dataset[1:35,], lineplot(Dias,
PT.dia24.CasosPorMilhão,
IT.dia33.CasosPorMilhão ,
SP.dia30.CasosPorMilhão,
GR.dia30.CasosPorMilhão,
FR.dia27.CasosPorMilhão))
with(Dataset[1:50,], lineplot(Dias,
PT.dia24.CasosPorMilhão,
IT.dia33.CasosPorMilhão ,
SP.dia30.CasosPorMilhão,
GR.dia30.CasosPorMilhão,
FR.dia27.CasosPorMilhão))
par(oldpar)
dev.off()
Dataset$IT.pred.bc.casos<-round(Dataset$IT.pred.bc*60461826/1000000,0)
Dataset$GR.pred.bc.casos<-round(Dataset$GR.pred.bc*83783942/1000000,0)
Dataset$FR.pred.bc.casos<-round(Dataset$FR.pred.bc*65273511/1000000,0)
Dataset$SP.pred.bc.casos<-round(Dataset$SP.pred.bc*46754778/1000000,0)
Dataset$PT.pred.bc.casos<-round(Dataset$PT.pred.bc*10196709/1000000,0)
Dataset$IT.casos<-round(Dataset$IT*60461826/1000000,0)
Dataset$GR.casos<-round(Dataset$GR*83783942/1000000,0)
Dataset$FR.casos<-round(Dataset$FR*65273511/1000000,0)
Dataset$SP.casos<-round(Dataset$SP*46754778/1000000,0)
Dataset$PT.casos<-round(Dataset$PT*10196709/1000000,0)
# Qualidade do modelo
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
plot(Dataset[complete.cases(Dataset$IT),]$IT,Dataset[complete.cases(Dataset$IT),]$IT.pred.bc)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$GR),]$GR,Dataset[complete.cases(Dataset$GR),]$GR.pred.bc)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$FR),]$FR,Dataset[complete.cases(Dataset$FR),]$FR.pred.bc)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$SP),]$SP,Dataset[complete.cases(Dataset$SP),]$SP.pred.bc)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$PT),]$PT,Dataset[complete.cases(Dataset$PT),]$PT.pred.bc)
abline(0,1,col="red")
par(oldpar)
dev.off()
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
with(Dataset, lineplot(Dias, PT, PT.pred.bc))
with(Dataset, lineplot(Dias, IT, IT.pred.bc))
with(Dataset, lineplot(Dias, SP, SP.pred.bc))
with(Dataset, lineplot(Dias, GR, GR.pred.bc))
with(Dataset, lineplot(Dias, FR, FR.pred.bc))
dev.off()
###################################
#LOG-LIN com pto de massa
###################################
IT<-lm(log(IT)~Dias, data=Dataset)
GR<-lm(log(GR)~Dias, data=Dataset)
FR<-lm(log(FR)~Dias, data=Dataset)
SP<-lm(log(SP)~Dias, data=Dataset)
PT<-lm(log(PT)~Dias, data=Dataset)
Dataset$IT.pred.lm<-exp(predict(IT,newdata=Dataset))
Dataset$GR.pred.lm<-exp(predict(GR,newdata=Dataset))
Dataset$FR.pred.lm<-exp(predict(FR,newdata=Dataset))
Dataset$SP.pred.lm<-exp(predict(SP,newdata=Dataset))
Dataset$PT.pred.lm<-exp(predict(PT,newdata=Dataset))
weqIT<-lm(Dataset$IT~Dataset$IT.pred.lm-1)
weqGR<-lm(Dataset$GR~Dataset$GR.pred.lm-1)
weqFR<-lm(Dataset$FR~Dataset$FR.pred.lm-1)
weqSP<-lm(Dataset$SP~Dataset$SP.pred.lm-1)
weqPT<-lm(Dataset$PT~Dataset$PT.pred.lm-1)
wIT<-summary(weqIT)$coef[1]
wGR<-summary(weqGR)$coef[1]
wFR<-summary(weqFR)$coef[1]
wSP<-summary(weqSP)$coef[1]
wPT<-summary(weqPT)$coef[1]
Dataset$IT.pred.lm<-wIT*Dataset$IT.pred.lm
Dataset$GR.pred.lm<-wGR*Dataset$GR.pred.lm
Dataset$FR.pred.lm<-wFR*Dataset$FR.pred.lm
Dataset$SP.pred.lm<-wSP*Dataset$SP.pred.lm
Dataset$PT.pred.lm<-wPT*Dataset$PT.pred.lm
#30.0 28.0 25.0 28.0 22.0
Dataset$IT.dia30.CasosPorMilhão<-c(Dataset[1:30,]$IT,Dataset[31:106,]$IT.pred.lm)
Dataset$GR.dia28.CasosPorMilhão<-c(Dataset[1:28,]$GR,Dataset[29:106,]$GR.pred.lm)
Dataset$FR.dia25.CasosPorMilhão<-c(Dataset[1:25,]$FR,Dataset[26:106,]$FR.pred.lm)
Dataset$SP.dia28.CasosPorMilhão<-c(Dataset[1:28,]$SP,Dataset[29:106,]$SP.pred.lm)
Dataset$PT.dia22.CasosPorMilhão<-c(Dataset[1:22,]$PT,Dataset[23:106,]$PT.pred.lm)
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(1, 3))
with(Dataset[1:22,], lineplot(Dias,
PT.dia22.CasosPorMilhão,
IT.dia30.CasosPorMilhão ,
SP.dia28.CasosPorMilhão,
GR.dia28.CasosPorMilhão,
FR.dia25.CasosPorMilhão))
with(Dataset[1:30,], lineplot(Dias,
PT.dia22.CasosPorMilhão,
IT.dia30.CasosPorMilhão ,
SP.dia28.CasosPorMilhão,
GR.dia28.CasosPorMilhão,
FR.dia25.CasosPorMilhão))
with(Dataset[1:40,], lineplot(Dias,
PT.dia22.CasosPorMilhão,
IT.dia30.CasosPorMilhão ,
SP.dia28.CasosPorMilhão,
GR.dia28.CasosPorMilhão,
FR.dia25.CasosPorMilhão))
par(oldpar)
dev.off()
Dataset$IT.pred.lm.casos<-round(Dataset$IT.pred.lm*60461826/1000000,0)
Dataset$GR.pred.lm.casos<-round(Dataset$GR.pred.lm*83783942/1000000,0)
Dataset$FR.pred.lm.casos<-round(Dataset$FR.pred.lm*65273511/1000000,0)
Dataset$SP.pred.lm.casos<-round(Dataset$SP.pred.lm*46754778/1000000,0)
Dataset$PT.pred.lm.casos<-round(Dataset$PT.pred.lm*10196709/1000000,0)
Dataset$IT.casos<-round(Dataset$IT*60461826/1000000,0)
Dataset$GR.casos<-round(Dataset$GR*83783942/1000000,0)
Dataset$FR.casos<-round(Dataset$FR*65273511/1000000,0)
Dataset$SP.casos<-round(Dataset$SP*46754778/1000000,0)
Dataset$PT.casos<-round(Dataset$PT*10196709/1000000,0)
#View(as.data.frame(cbind(Dataset$PT.casos,Dataset$PT.pred.lm.casos)))
#View(as.data.frame(cbind(Dataset$IT.casos,Dataset$IT.pred.lm.casos)))
#with(Dataset[1:31,], lineplot(Dias, IT, IT.pred.lm))
############################
#COMPARAÇÃO DE CRESCIMENTO DE PT E IR LOG LIN. Toda a amostra
# confirmar
############################
# oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(1, 2))
#
# nn<-sum(complete.cases(Dataset$PT))
#
# betas.exponencialPT<-rep(NA,(nn-7))
#
#
# for(ii in 7:nn){
#
# PT<-lm(log(PT)~Dias, data=Dataset[1:ii,])
#
# betas.exponencialPT[ii-7]<-summary(PT)$coef[2]
# }
#
# plot(seq(from=8,to=nn,by=1),betas.exponencialPT,
# main = "PT:: Taxa de crescimento, usando todos os dados desde o dia 8 em diante",
# xlab="Dia de crise",
# ylab="beta da regressão: log(casos permilhao)=constante +B * Dias",
# type = "o",col="red",
# )
#
#
#
# nn<-sum(complete.cases(Dataset$IT))
#
# betas.exponencialIT<-rep(NA,(nn-7))
#
#
# for(ii in 7:nn){
#
# IT<-lm(log(IT)~Dias, data=Dataset[1:ii,])
#
# betas.exponencialIT[ii-7]<-summary(IT)$coef[2]
# }
#
# plot(seq(from=8,to=nn,by=1),betas.exponencialIT,
# main = "IT:: Taxa de crescimento, usando todos os dados desde o dia 8 em diante",
# xlab="Dia de crise",
# ylab="beta da regressão: log(casos permilhao)=constante +B * Dias",
# type = "o",col="red",
# )
#
#
# par(oldpar)
#
#
# dias<-seq(from=8,to=sum(complete.cases(Dataset$IT)),by=1)
# betas.exponencialPT<-
# c(betas.exponencialPT,
# rep(NA,
# sum(complete.cases(Dataset$IT))
# -sum(complete.cases(Dataset$PT))
# )
# )
#
# betas.exponencialIT<-betas.exponencialIT
#
# aux<-as.data.frame(cbind(dias,betas.exponencialPT,betas.exponencialIT))
#
# with(dias, lineplot(aux, betas.exponencialIT, betas.exponencialPT))
#
#
############################
#comparar taxa de crescimento PT vs IT
############################
nn<-sum(complete.cases(Dataset$PT))
betas.exponencialPT<-rep(NA,(nn-7))
for(ii in 8:nn){
aa=ii-7
PT<-lm(log(PT)~Dias, data=Dataset[aa:ii,])
betas.exponencialPT[ii-7]<-summary(PT)$coef[2]}
nn<-sum(complete.cases(Dataset$IT))
betas.exponencialIT<-rep(NA,(nn-7))
for(ii in 8:nn){
aa=ii-7
IT<-lm(log(IT)~Dias, data=Dataset[aa:ii,])
betas.exponencialIT[ii-7]<-summary(IT)$coef[2]}
dias<-seq(from=8,to=sum(complete.cases(Dataset$IT)),by=1)
betas.exponencialPT<-
c(betas.exponencialPT,
rep(NA,
sum(complete.cases(Dataset$IT))-sum(complete.cases(Dataset$PT))
)
)
betas.exponencialIT<-betas.exponencialIT
aux<-as.data.frame(cbind(dias,betas.exponencialPT,betas.exponencialIT))
with(aux, lineplot(dias, betas.exponencialPT,betas.exponencialIT))
dev.off()
library(rio)
write.csv(Dataset,"C:\\Lixo\\Dataset.xls")
############################
#Qualidade do modelo log lin com massa
############################
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
plot(Dataset[complete.cases(Dataset$IT),]$IT,Dataset[complete.cases(Dataset$IT),]$IT.pred.lm)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$GR),]$GR,Dataset[complete.cases(Dataset$GR),]$GR.pred.lm)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$FR),]$FR,Dataset[complete.cases(Dataset$FR),]$FR.pred.lm)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$SP),]$SP,Dataset[complete.cases(Dataset$SP),]$SP.pred.lm)
abline(0,1,col="red")
plot(Dataset[complete.cases(Dataset$PT),]$PT,Dataset[complete.cases(Dataset$PT),]$PT.pred.lm)
abline(0,1,col="red")
par(oldpar)
############################
#logistic.dxl - 100%
# não usar - talvez para Holanda e UK
# apenas meio feito
############################
#
#
# logistic.dxl <- function(p,x,unidade) {
#
# p<-(p)/unidade
# odds<-p/((1-p))
# log.odds<-log(odds)
# df<-as.data.frame(x)
# aux1<-lm(log.odds~x)
# log.odds.pred<-predict.lm(aux1,newdata=df)
# odds.pred<-exp(log.odds.pred)
# p.pred<-odds.pred/(1+odds.pred)
#
# return(p.pred*unidade)
# }
#
# IT<-logistic.dxl(Dataset$IT,Dataset$Dias,1000000)
# GR<-logistic.dxl(Dataset$GR,Dataset$Dias,1000000)
# FR<-logistic.dxl(Dataset$FR,Dataset$Dias,1000000)
# SP<-logistic.dxl(Dataset$SP,Dataset$Dias,1000000)
# PT<-logistic.dxl(Dataset$PT,Dataset$Dias,1000000)
#
#
# lineplot(Dataset$Dias,PT,IT,GR,FR,SP)
#
# max(PT)
############################
#logistic 2
############################
library("drc")
#https://stackoverflow.com/questions/43562591/r-fit-logistic-curve-through-a-scatterplot/43564372
#https://rstats4ag.org/dose-response-curves.html
#https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4696819/
IT.log <- drm(IT ~ Dias, data = Dataset, fct = L.3(), type = "continuous") #para log-logistica colocar LL
GR.log <- drm(GR ~ Dias, data = Dataset, fct = L.3(), type = "continuous") #para log-logistica colocar LL
FR.log <- drm(FR ~ Dias, data = Dataset, fct = L.3(), type = "continuous") #para log-logistica colocar LL
SP.log <- drm(SP ~ Dias, data = Dataset, fct = L.3(), type = "continuous") #para log-logistica colocar LL
PT.log <- drm(PT ~ Dias, data = Dataset, fct = L.3(), type = "continuous") #para log-logistica colocar LL
dias.de.crise.em.pt<-sum(complete.cases(Dataset$PT))
dias.de.crise.em.pt.1<-dias.de.crise.em.pt-1
dias.de.crise.em.pt.2<-dias.de.crise.em.pt-2
PT.log1 <- drm(PT ~ Dias, data = Dataset[1:dias.de.crise.em.pt.1,], fct = L.3(), type = "continuous") #para log-logistica colocar LL
PT.log2 <- drm(PT ~ Dias, data = Dataset[1:dias.de.crise.em.pt.2,], fct = L.3(), type = "continuous") #para log-logistica colocar LL
#confirmar
logistic.dxl<-function(x, b,c, d, e){#L.3 na eq acima
return(c+
(d-c)/((1+exp(
b*(
(x)-(e)
)
)
))
)
}
log.logistic.dxl<-function(x, b,c, d, e){#LL.3 na eq acima
return(c+
(d-c)/((1+exp(
b*(
log(x)-log(e)
)
)
))
)
}
Dataset$IT.pred.log<-(predict(IT.log,newdata = Dataset))
Dataset$GR.pred.log<-(predict(GR.log,newdata = Dataset))
Dataset$FR.pred.log<-(predict(FR.log,newdata = Dataset))
Dataset$SP.pred.log<-(predict(SP.log,newdata = Dataset))
Dataset$PT.pred.log<-(predict(PT.log,newdata = Dataset))
Dataset$PT.pred.log1<-(predict(PT.log1,newdata = Dataset))
Dataset$PT.pred.log2<-(predict(PT.log2,newdata = Dataset))
xxxx<-(log.logistic.dxl(Dataset$Dias,
summary(PT.log)$coef[1],
0,
summary(PT.log)$coef[2],
summary(PT.log)$coef[3]))
#plot(xxxx)
yyyy<-(logistic.dxl(Dataset$Dias,
summary(PT.log)$coef[1],
0,
summary(PT.log)$coef[2],
summary(PT.log)$coef[3]))
dev.off()
plot(Dataset$PT.pred.log,yyyy)
abline(0,1)
Dataset$IT.pred.log.casos<-round(Dataset$IT.pred.log*60461826/1000000,0)
Dataset$GR.pred.log.casos<-round(Dataset$GR.pred.log*83783942/1000000,0)
Dataset$FR.pred.log.casos<-round(Dataset$FR.pred.log*65273511/1000000,0)
Dataset$SP.pred.log.casos<-round(Dataset$SP.pred.log*46754778/1000000,0)
Dataset$PT.pred.log.casos<-round(Dataset$PT.pred.log*10196709/1000000,0)
dev.off()
oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
with(Dataset[1:50,], lineplot(Dias, IT, IT.pred.log))
with(Dataset[1:50,], lineplot(Dias, GR, GR.pred.log))
with(Dataset[1:50,], lineplot(Dias, FR, FR.pred.log))
with(Dataset[1:50,], lineplot(Dias, SP, SP.pred.log))
with(Dataset[1:50,], lineplot(Dias, PT, PT.pred.log))
with(Dataset[1:50,], lineplot(Dias
,PT.pred.log
,IT.pred.log
,SP.pred.log
,GR.pred.log
,FR.pred.log
))
par(oldpar)
horizonte=40
temp.decorrido=24
plot (Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$PT.pred.log,ylim=c(0,2500),xlab="dias de crise",ylab="casos por milhão", col="black", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$SP.pred.log,col="orange", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$GR.pred.log,col="red", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$IT.pred.log,col="green", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$FR.pred.log,col="blue", type="b")
legend(1, 2400, legend=c("Portugal", "Espanha","Alemanha","Itália","França"),
col=c("black", "orange", "red", "green","blue"), lty=1:2, cex=0.8)
plot (Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$PT.pred.log,ylim=c(0,800),xlab="dias de crise",ylab="casos por milhão", col="black", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$PT.pred.log1,col="red", type="b")
lines(Dataset[1:horizonte,]$Dias,Dataset[1:horizonte,]$PT.pred.log2,col="blue", type="b")
abline(v=dias.de.crise.em.pt, col="grey")
legend(1, 750, legend=c("Portugal - previsão ao dia de hoje", "Portugal - previsão ao dia de ontem",
"Portugal - previsão ao dia de anteontem",
paste0("Dia de crise (hoje): ",dias.de.crise.em.pt,".º")),
col=c("black", "red", "blue","grey"), lty=1:2, cex=0.8)
Dataset$D.PT.pred.log <- c(NA,diff(Dataset$PT.pred.log,differences = 1))
Dataset$D.PT.pred.log.casos <- c(NA,diff(Dataset$PT.pred.log.casos,differences = 1))
dev.off()
with(Dataset[1:50,], lineplot(Dias
,PT
,PT.pred.log
,D.PT.pred.log
))
dev.off()
horizonte=40
temp.decorrido=23
max<-Dataset$Dias[which.max(Dataset$D.PT.pred.log.casos)]
plot(x = Dataset[1:horizonte,]$Dias, y = Dataset[1:horizonte,]$PT.pred.log.casos, col="blue",ylab="N.º de casos",xlab="Dias desde o início da crise",type="l")
lines(x = Dataset[1:temp.decorrido,]$Dias, y = Dataset[1:temp.decorrido,]$PT.casos,type="p")
lines(x = Dataset[1:horizonte,]$Dias, y = Dataset[1:horizonte,]$D.PT.pred.log.casos, col="red")
abline(a=NULL, b=NULL, h=NULL, v=temp.decorrido, col="grey")
#abline(a=NULL, b=NULL, h=NULL, v=max, col="dark grey")
legend(1, 6000, legend=c("Portugal - evolução prevista (ao dia de hoje) para o total de casos (acumulado)"
,"Portugal - evolução real do total de casos (acumulado)"
,"Portugal - evolução de novos casos"
,paste0("Dia de crise (hoje): ",dias.de.crise.em.pt,".º")
#,paste0("Pico de novos casos")
),
col=c("black"
,"red"
,"blue"
,"grey"
#,"dark grey"
), lty=1:2, cex=0.8)
# oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
# with(Dataset, lineplot(Dias, IT.casos, IT.pred.log.casos))
# #with(Dataset, lineplot(Dias, GR.casos, GR.pred.log.casos))
# with(Dataset, lineplot(Dias, FR.casos, FR.pred.log.casos))
# with(Dataset, lineplot(Dias, SP.casos, SP.pred.log.casos))
# with(Dataset, lineplot(Dias, PT.casos, PT.pred.log.casos))
#
# with(Dataset, lineplot(Dias,
# PT.pred.log.casos,
# IT.pred.log.casos,
# SP.pred.log.casos,
# GR.pred.log.casos,
# FR.pred.log.casos
# )
# )
#
# par(oldpar)
max(Dataset$IT.pred.log.casos)/1000
max(Dataset$GR.pred.log.casos)/1000
max(Dataset$FR.pred.log.casos)/1000
max(Dataset$SP.pred.log.casos)/1000
max(Dataset$PT.pred.log.casos)/1000
export(Dataset,"C:/lixo/Dataset.xlsx")
############################
#SUR - LIXO
############################
# ####
# IT<-(log(IT)~+Dias)
# GR<-(log(GR)~Dias)
# FR<-(log(FR)~Dias)
# SP<-(log(SP)~Dias)
# PT<-(log(PT)~Dias)
#
# IT <- (powerTransform(IT, lambda.IT) ~ Dias)
# GR <- (powerTransform(GR, lambda.GR) ~ Dias)
# FR <- (powerTransform(FR, lambda.FR) ~ Dias)
# SP <- (powerTransform(SP, lambda.SP) ~ Dias)
# PT <- (powerTransform(PT, lambda.PT) ~ Dias)
#
# eqSystem <- list(IT ,GR, FR, SP, PT)
# sur<-systemfit( eqSystem, method = "SUR", data = Dataset )
#
# summary(sur)
#
# sur.col<-(predict(sur,dataset=Dataset))
# names(sur.col)<-c("IT.pred", "GR.pred", "FR.pred", "SP.pred", "PT.pred")
#
# #Dataset$IT.pred.SUR<-exp(sur.col$IT.pred)
# #Dataset$GR.pred.SUR<-exp(sur.col$GR.pred)
# #Dataset$FR.pred.SUR<-exp(sur.col$FR.pred)
# #Dataset$SP.pred.SUR<-exp(sur.col$SP.pred)
# #Dataset$PT.pred.SUR<-exp(sur.col$PT.pred)
#
# Dataset$IT.pred.SUR<-InversePowerTransform(sur.col$IT.pred,lambda.IT)
# Dataset$GR.pred.SUR<-InversePowerTransform(sur.col$GR.pred,lambda.GR)
# Dataset$FR.pred.SUR<-InversePowerTransform(sur.col$FR.pred,lambda.FR)
# Dataset$SP.pred.SUR<-InversePowerTransform(sur.col$SP.pred,lambda.SP)
# Dataset$PT.pred.SUR<-InversePowerTransform(sur.col$PT.pred,lambda.PT)
#
#
# names(Dataset)
#
# weqIT<-lm(Dataset$IT~Dataset$IT.pred.SUR-1)
# weqGR<-lm(Dataset$GR~Dataset$GR.pred.SUR-1)
# weqFR<-lm(Dataset$FR~Dataset$FR.pred.SUR-1)
# weqSP<-lm(Dataset$SP~Dataset$SP.pred.SUR-1)
# weqPT<-lm(Dataset$PT~Dataset$PT.pred.SUR-1)
#
# wIT<-summary(weqIT)$coef[1]
# wGR<-summary(weqGR)$coef[1]
# wFR<-summary(weqFR)$coef[1]
# wSP<-summary(weqSP)$coef[1]
# wPT<-summary(weqPT)$coef[1]
#
#
# Dataset$IT.pred<-wIT*Dataset$IT.pred.SUR
# Dataset$GR.pred<-wGR*Dataset$GR.pred.SUR
# Dataset$FR.pred<-wFR*Dataset$FR.pred.SUR
# Dataset$SP.pred<-wSP*Dataset$SP.pred.SUR
# Dataset$PT.pred<-wPT*Dataset$PT.pred.SUR
#
#
# oldpar <- par(oma = c(0, 0, 3, 0), mfrow = c(2, 3))
#
# plot(Dataset$IT,Dataset$IT.pred.SUR)
# abline(0,1,col="red")
#
# plot(Dataset$GR,Dataset$GR.pred.SUR)
# abline(0,1,col="red")
#
# plot(Dataset$FR,Dataset$FR.pred.SUR)
# abline(0,1,col="red")
#
# plot(Dataset$SP,Dataset$SP.pred.SUR)
# abline(0,1,col="red")
#
# plot(Dataset$PT,Dataset$PT.pred.SUR)
# abline(0,1,col="red")
#
# par(oldpar)
#
#
# with(Dataset, lineplot(Dias, PT, PT.pred))
# with(Dataset, lineplot(Dias, IT, IT.pred))
PwC Scale #InsurTech programme - executive evening
Check the fotos
Scale | InsurTech
***
Hi everyone
My name is Filipe Charters, and I’m the CEO of Data XL
We love the insurance sector; we believe that insurance companies have much to give to the world
Our business model is to provide tools - essentially insurance pricing tools – that make insures rock.
Today we bring to you our two flagship products.
. SUPPLIER OVERCHARGE DETECTION – a special case of fraud.
. Price optimization with an API
An optimal price is a price that optimizes the margin, the revenue OR minimizes the churn.
Insures companies define price in the following way:
(SLIDE)
. They sum all costs, and they say they a price. When you sum all costs, you have the total cost.
. insurers put the price near the cost, we want to put the price near the value.
This is why an IPHONE costs twice as much as a Samsung, even though the raw material is the same.
(SLIDE)
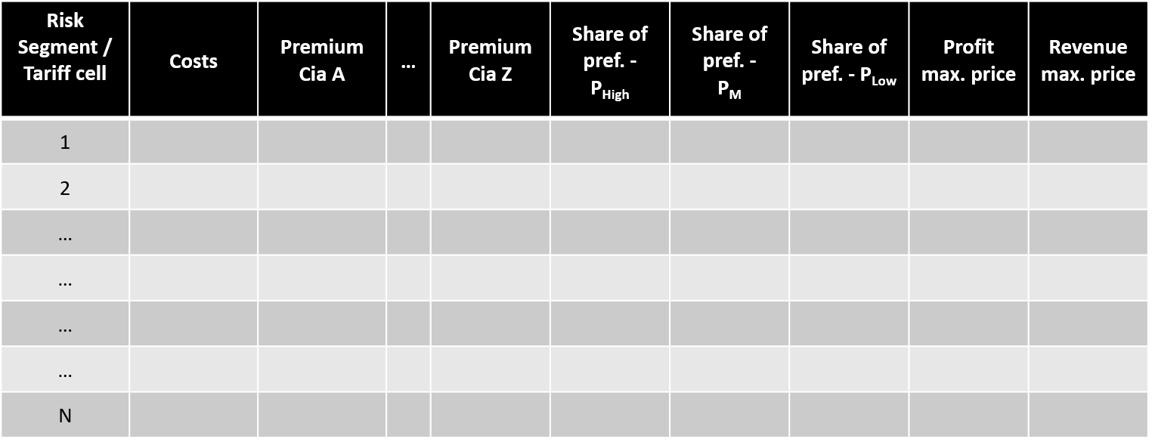
So, we build this platform, where insurance companies can put all their renewals information and receive the optimal price back.
The same input with same extra columns:
- The price that max the revenue
- The price that max the margin
- The price that minimizes the churn
This platform is working now. It’s secure – it’s cloud base in a world class provider (digital ocean), but it can be stuck in your servers.
We do not define the strategy!! So, I cannot talk about the financials, but we can imagine what would mean for a price increase of 1%, maintain the same renewal rate.
As to accuracy we can say that our margin of error was more or less 2 %.
Just 2%.
(SLIDE)
Why are we different?
To make this happen we need:
. the risk numbers (which insures already have), the price of the competition and the will 2 pay model.
We developed some algorithms where we can reverse engineer the price of the competition.
And with very good experimental design we measure the will to pay.
No current provider offers this at the same time.
Also, our competitors offer a software and a manual.
Not a solution.
(SLIDE)
Are we compliance with the FSA for a transparent price?
. YES. We work with segments, so each policyholder with the same characteristics will receive the same price.
. We are fair, but efficient. If you need to lower your price, we can say how much lower should your price quote be.
If you want to charge more, we can say the optimal price.
(SLIDE)
Now let’s talk about abuse.
We are running out of time, let me be efficient.
The current anti-fraud procedure is: look to the surroundings around a claim.
We look to the provider. The health provider. The car repair shop.
Imagine that a maternity hospital makes a lot of c-section. Each and everyone can have the proper patter and medical justification.
But the overall expense will be higher, but above all the digit distribution in the expense will be different.
Imagine that a provider needs clinical authorization for expenses above 2000 pounds.
Whenever a doctor wants to make this specific procedure, he will split the expenses in two invoices.
With our algorithm we will be able to detect this overcharge, since we will analyse the digits that compose each invoice.
And what we're going to see that we have more expenses started with the digit “1 " than we would expect
(SLIDE)
You see, there is a statistical law for the leading digits.
We know that the digit 1 will appear as a leading digit in 30% of the time. As the digit 9, for example, will appear less than 5% as a leading digit.
(SLIDE)
We can take this a step further and check if the digits follow the right distribution.
For instances in this example we check the first two digits of every invoice follow the proper distribution (is the red line).
And we can see that expenses that there are too many invoices that starts with “2 and a 5”
(SLIDE)
As a result, we have a 66% accuracy of finding overcharge on providers-
(SLIDE)
We are making money with these two products
We have credentials that we can share.
Came talk to us
Let’s run a pilot
A marca "Data XL" é nossa!
«Big Data Is A Sham» - a must read
Check the full article here.
POR OS NÚMEROS NO CENTRO DA COMPANHIA
No meio de legislação e normas, há às vezes algumas supresas: "Tenho a certeza que as seguradoras sabem que têm de ser mais do que uma commodity: o desafio está em como o ser..." - o meu artigo na newsletter da APS
The other side of the coin....
- "I want to optimize my price!"
- "Sure!, More revenue, more margin, more policies - what is your goal?"
- "Minimize the cost, subject to this renewal share"
Minimize cost! Yes! So obvious now!

Photo credits: By Andrè Bellingrodt - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=39375494
Proudly presenting Lazarus - our new product for winning-back former customers
Check out our business case simulator and let us know what you think!
*
You know that the client has left the company.
You know that it's necessary to present a lower price.
But how low should the price be?
Data XL allows insurers to setup the win-back price!
Brouchure here.
Business case simulater here.
Demo day - Pitch :: Dec - 2017
Our pitch for @F10_accelerator at #F10Demo: insurance pricing optimization!
HERE
Insurance Pricing Room is Live!!!! *vs1.0
"Get inspired by DataXL" by SIX
Hi!
Please check a quick interview made by SIX about Data XL
Every year F10 (powered by SIX) supports thirty startups to make the jump from idea to registered company. In this interview, for the internal the internal comm channel, SIX do not ask about business models, but about the people behind the ideas: "What drives them? Where do they find inspiration and how do they see the future?"
Hope you like it!
(a full transcript below)


**************
Every year F10 supports thirty
startups to make the jump from idea to registered company. In this weekly
series, we will not talk about business models, but about the people behind the
ideas. What drives them? Where do they find inspiration and how do they see the
future?
Here are 5 questions we asked to Filipe Charters de Azevedo who, when asked to compares his start-up with a fruit, choose a banana: because it would have a big smile and life is full of slippery falls.
- Who is the person that most inspires you and why?
The one person that has helped me most in my journey through life is, of course, my wife. But I do not want to be too sentimental in a business interview, so I will tell you about the books that have changed my professional view:
Information Rules: A Strategic Guide to the Network Economy, by Carl Shapiro and Hal Varian. They argue that if managers seriously want to develop effective strategies for competing in the new marketplace, they must understand the fundamental economics of information technology. I almost called the company "Data Rules," because of this book.
The Third Wave by Alvin Toffler allowed me a glimpse into the future. The book was written in the 1970s, and I am still surprised how accurate Toffler’s predictions of our time were.
2. How did you get the idea to start DataXL?
There was neither a eureka moment nor an apple falling on my head. The company is the product of a lot of thinking about how to combine expertise (experimental design), market (insurance and financial sector) and distribution (SaaS). Now it is easy to put in one sentence…
3. How is life in F10?
It is like being in the Erasmus program, but for grown-up entrepreneurs. At home in Portugal, after work, I would usually drink a coffee and eat a “pastel de nata” with my friends and colleagues. Here we drink beer!
4. Did you always want to become an entrepreneur?
I believe that
I’m what is called a T-person. The vertical bar on the T represents the depth
of related skills and expertise in a single field, whereas the horizontal bar
is the ability to collaborate across disciplines with experts in other areas
and to apply knowledge in areas of expertise other than one's own.
Usually people are “I” people: experts with
in-depth knowledge; a quality that companies appreciate and reward. But if you
have the ability to collaborate across areas it becomes easier to see the big
picture and create a company. Developing a new concept becomes the next natural
step. Becoming an entrepreneur is for most “T” people the only way to feel
satisfied.
5. Complete the following sentence: In five years' time…
…I'll have no regrets. Not even a few to mention.
Founder Box
Filipe Chartes de Azevedo (39) is a Portuguese entrepreneur with a background in consulting. Last year he founded the company Data XL, an online tool used for insurance pricing optimization.
Data XL is on PwC radar
Check it out!!!
"The breadth of InsurTech is impressive. The challenge for these new entrants over the next year is to start to scale. The challenge for incumbents is how to embrace these new players and fit them into new business models. Only then will the full potential of this transformation be realised and the InsurTech picture be clear."
source: https://www.linkedin.com/pulse/insurtech-started-blank-canvas-jonathan-howe/?trackingId=ZgbaBwrI8gMHizb8JP7fgA%3D%3D

How to refocus the PT ailing Workers Comp portfolio?

In Portugal, the Works Comp is stressing companies' results excessively. The problem is essentially a problem of tariff setting. "How to refocus the PT ailing Workers Comp portfolio?" is the question we try to answer.
It is a reflection on what can be done, presenting concrete measures.
All feedback is welcome.
---------------------------
Trata-se de uma reflexão serena sobre o que pode ser feito, apresentando medidas concretas.
Todos os contributos são bem vindos.
---------------------------
Insurance Princing Room
Our product was born from the need of Insurers to find out what customers value their products. With our solution, it is now possible for Insurers to identify which properties of their products do customers value the most and more importantly how much are they willing to pay for them.
Introducing Dynamic Pricing to Insurance - Meet Insurtech DataXL
We at Data XL help insurance companies to charge more if they can, less if they must.
We offer INSURANCE PRICE OPTIMIZATION WITH API.
@SuperDaveBruno! made a quick interview about our project on Data XL! Thank you for challenging us, to spread the message.
*
"DataXL can help you increase revenues by 2-4% in the first pilot. So if you're an Insurer looking for effective Insurtech Startups - you just found one. DataXL uses the same modern data analysis and logic applied by the big online retailers (eg. Amazon, eBay). Phil Charters, CEO of DataXL is helping bring Insurance into the digital age. DataXL uses algorithms during your renewals process to see where a customer perceives more value - and you can increase pricing.
.
My name is David Bruno and I am an entrepreneur, startup coach and investor."
DataXL - Value Based Pricing - Pitch
Have you ever wondered why an iPhone costs twice as much as a Samsung?
Correlation is not causation!
Know one of our secret sources - and the limitations of using only internal data. This 2-minute video (kind of...) explains where and why Big Data cannot solve everything in an internal meeting at F10.
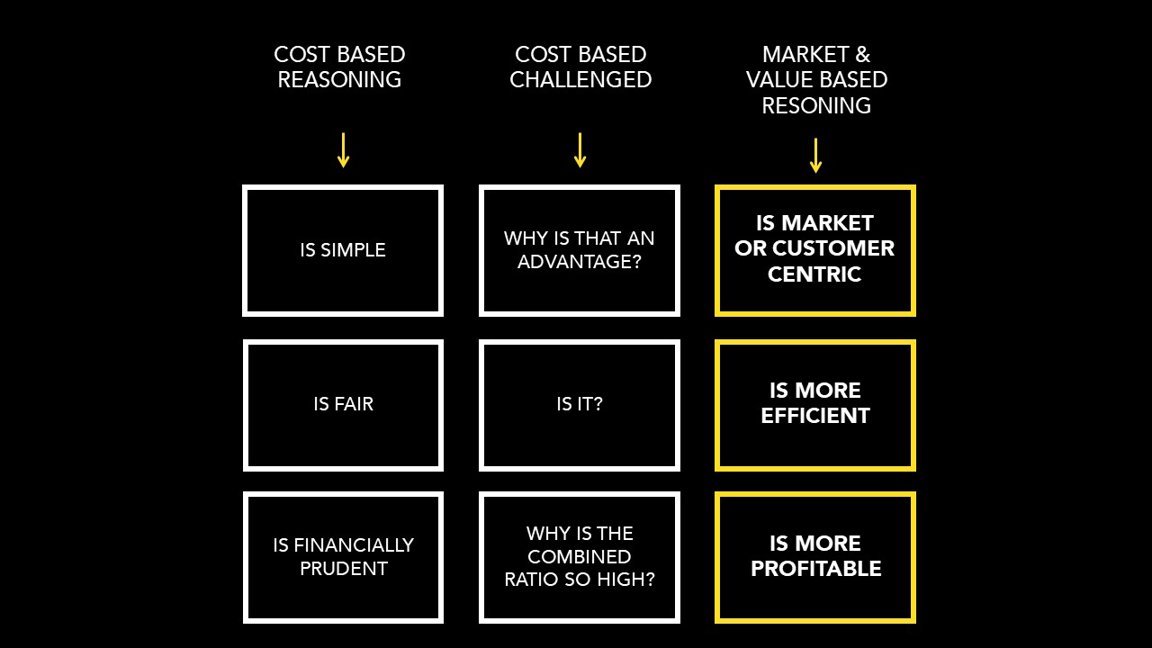
Let's challenge the Cost Based Reasoning
Cost-plus pricing is used primarily because it is easy to calculate and requires little information.
Insurance companies say it is fairer and financial prudent.
Check our views below!